오식랜드
데이터 사이언스 본문
반응형
머신러닝
기초
알고리즘 : 문제 해결을 위한 절차나 방법
머신러닝 : 기계가 패턴을 학습하여 자동화하는 알고리즘
- 지도학습 : 문제와 답을 함께 학습
- 회귀 (연속형) : y 특징 찾아 데이터 x 이용해 y 예측 (ex. 키, 몸무게)
- 분류 (이산형) : dog or cat
- 비지도학습 : 컴퓨터 스스로 학습
- 군집 (클러스터) : 모델이 스스로 분류 기준을 찾아 집단 구분
⇒ 실제 답(ground truth)인 y의 존재 여부에 따라 학습 방법 구분
기본 모형 (model) : y = f(x)
ex) 키를 이용해 몸무게 예측? y=f(x)라는 머신러닝 모델을 통해 예측 할 수 있다
통계 붙석 및 전처리 라이브러리
- 넘파이 (Numpy) : 선형대수 계산식을 파이썬으로 구현
- 판다스 (Pandas) : 넘파이 기반, 사실상 표준 라이브러리 (데이터 전처리, 통계, 엑셀, 피봇 테이블 등)
- 사이파이 (Scipy) : 넘파이 기반, 거의 모든 수학 연산
- 매트플롯립 (Matplotlib) : 대중적 그래프 생성 라이브러리
데이터 명칭
- 데이터 테이블 (data table) : 데이터 표
- 독립 변수 x (feature) : 종속변수 y에 영향을 주는 특성
- = 열 이름 (column name)
- 데이터 인스턴스 (data instance)
- 데이터 1개 묶음
- 튜플(tuple)
- 엑셀 1줄 (행)
- 연속형 데이터 (숫자형 데이터)
- 온도, 키, 몸무게 등
- 값이 끊어지지 않음 (값 a와 b사이 무한한 수 존재 가능
- 이산형 데이터 (명목형 데이터)
- 성별, 주소, 설문조사 척도
- 값이 라벨의 역할 수행
- 숫자의 의미가 없음
⇒ 숫자의 의미가 스케일(scale)이 있는가, 없는가로 구분
⇒ scale : *10, *100을 해도 의미가 있는가 없는가
- 숫자형 데이터
- 등간 척도형 : 단위(m)
- 비율 척도형 : 데이터와 비율
- 정량적 측정, 정수나 실수 값
- 명목형 데이터
- 카테고리로 분류 가능
- 명목 척도
- 서수형 데이터
- 범주형 데이터 + 데이터 간 순서 존재
- 대 / 중 / 소
- 비례하지는 않음
차원의 저주
- feature 개수가 크게 증가 → 차원 증가 → 표현 불가
- 희박한 벡터 생성 (sparse vector) : 벡터 공간에 0이 너무 많이 포함된 상태 → 정확도 떨어짐
- 데이터 처리 속도 감소 / 메모리 공간 많이 차지 → 샘플 데이터가 많아져 발생
NumPy
- 사실상 표준 라이브러리
- 선형대수 표현법을 코드로 처리 (벡터, 행렬)
- 다차원 리스트 등 크기가 큰 데이터 처리에 유리
- 속도가 빠르고 메모리 사용 효율적
- 반복문X 병렬로 처리O
텐서
: 선형대수의 데이터 배열
랭크(Rank) 이름
| 0 | 스칼라 |
| 1 | 벡터 |
| 2 | 행렬 |
| 3, … , n | n차원 텐서 |
함수
tensor_rank3 = [[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2,
5, 8]], [[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],
[[1, 2, 5, 8], [1, 2, 5, 8], [1, 2, 5, 8]],[[1, 2,
5, 8], [1, 2, 5, 8], [1, 2, 5, 8]] ]
np.array(tensor_rank3, int).ndim ==> 3 : RANK 출력
np.array(tensor_rank3, int).size ==> 48 : 원소 총 갯수
np.array( [[1, 2, 3.5], [4, 5, 6.5]], dtype=float)
==> data type 변경
==> [[1., 2., 3.5], [4., 5., 6.5]] 로 변경
- ndim : rank 출력
- size : 원소 총 갯수 출력
- dtype / type : 데이터 타입 변경
x = np.array([[1, 2, 5, 8], [1, 2, 5, 8]])
x.shape ==> (2, 4)
x.reshape(-1,) 혹은 x.flatten()
==> 벡터로 바꿔준다
==> array([1, 2, 5, 8, 1, 2, 5, 8])
x = np.array(range(8)).reshape(4,2)
==> array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
- reshape : 행렬 크기 변경
- flatten : 1차원 벡터로 변경
*중요함수
- diag : 대각성분 값 추출 (k는 시작 인덱스)
- uniform : 균등분포 함수
슬라이싱 (행, 열)
x = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]], int)
- x [ : , 2 : ]
- array([[ 3, 4, 5], [ 8, 9, 10]])
- x [ 1 , 1 : 3 ]
- array([7, 8])
- x [ 1 : 3 ]
- array([[ 6, 7, 8, 9, 10]])
브로드캐스팅 연산
- 2x3 텐서와 1개의 스칼라 곱 → 텐서 모든 원소마다 스칼라 값 곱
Pandas
groupby
df.groupby("Team")["Points"].sum()
df.groupby(나누는 기준)[연산 대상].함수()
- 분할 → 적용 → 결합 과정
- 대/소문자 구분
- agg(min) , agg(mean) → agg 함수를 통해 기존 함수 사용
- transform(max) → 제일 큰 값으로 통일
lambda
lambda x: (x - x.mean()) / x.std()
df.groupby('Team').filter(lambda x: x["Points"].max() > 800)
- lambda : 함수 → 객체 변환
- Ʃ0 → NaN : 평균과 자기 자신이 같아서 → 표준편차 : 0
병합
- 내부 조인 (inner) : 교집합 (Default)
- 완전 조인 (full) : 합집합
- 왼쪽 조인 : 왼쪽 그룹 + 교집합
- 오른쪽 조인 : 오른쪽 그룹 + 교집합
- 키 값 선택 : on
pd.merge(left=df_left, right=df_right, how="inner", on='subject_id')
pd.merge(left=df_left, right=df_right, left_on='left_id', right_on='right_id')
연결
- 주로 세로로 데이터 연결
- concat : 2개 이상을 한번에 합칠 때
- append : 기존 테이블에 다른 테이블 1개를 붙일 때 (2개씩)
Matplotlib
- 데이터 시각화 모듈
- 레이어를 쌓듯이 쌓음
- plt객체 - figure (그림) 객체 - axes (축) 객체
함수
- plt.show() : 마지막에 호출해야 출력
- 축 만들기
- add_subplot
- ax_1 = fig.add_subplot(1, 2, 1) → 1행 2열로 나눈 후 1번
- ax_2 = fig.add_subplot(1, 2, 2) → 1행 2열로 나눈 후 2번
- subplots
- fig, ax = plt.subplots(nrows=1, ncols=2)
- fig, ax = plt.subplots(2, 2)
집합 표현법
- 원소 나열법 : {1, 2, 3, 4, 5}
- → a = [1, 2, 3, 4, 5]
- 조건 제시법 : { x | x는 12의 약수 }
- → a = [ x for x in range(1, 13) if 12 %x == 0 ]
산점도
데이터 분포도를 2차원 평면에 도형으로 표현
막대그래프
# (3) 3개의 막대그래프 생성
plt.bar(X + 0.00, data[0], color = 'b', width = 0.50)
plt.bar(X + 0.50, data[1], color = 'g', width = 0.50)
plt.bar(X + 1.0, data[2], color = 'r', width = 0.50)
# (4) X축에 표시될 이름과 위치 설정
plt.xticks(X+0.50, ("A","B","C", "D"))
누적 막대그래프 (아래서부터 쌓이는 것)
for i in range(3):
plt.bar(X, data[i], bottom = np.sum(data[:i], axis=0), color = color_list[i], label=data_label[i])
히스토그램
- 데이터 분포 확인
- bins : x축 구간
- boxplot : 상자그림
- 0% -[ 25%(Q1) - 50%(중앙값) - 75%(Q3) ]- 100%
- boxplot 이외는 “이상치” (outliers) 라고 한다
데이터 전처리 / 정규화
- 데이터의 최대값과 최솟값을 0~1 사이 값으로 바꿔준다
- 표준 정규분포 형태로 나타낸다
*너무 큰 수 * 너무 작은 수 → round off error
결측치 처리
- 삭제 (drop)
- 데이터가 없는 열이나 행 삭제
- dropna()
- 원본 df은 불변
- inplace=True 쓰면 원본 수정
- how 파라미터
- any : 하나의 NaN만 있어도 삭제 (Default)
- all : 모든 값이 NaN일 때 삭제
- 채우기 (fill)
- 평균값, 최빈값, 중간값 등으로 데이터를 채움
- fillna()
- 원본 df은 불변
- inplace=True 쓰면 원본 수정
- df["preTestScore"].mean() 와 같이 해당 열의 평균이나 중간값 등으로 채워준다
- df.isnull().sum() / len(df) : 얼마나 비어있는지 퍼센트로 출력
- threshfh : 개수를 기준으로 삭제 (thresh=1 → 한 개 이상 존재하면 남기기 (all과 같이 동작))
- groupby와 함께 사용
- : 성별로 구분지어 점수를 모두 평균으로 바꿈
df.groupby("sex")["postTestScore"].transform("mean")
df["postTestScore"].fillna(df.groupby("sex")["postTestScore"].transform("mean"), inplace=True)
원핫 인코딩
- 머신러닝 사용 시 범주별 가능성을 표기하기 위해 사용
- get_dummies로 구현 가능
- 대괄호[ ] 차이
- pd.get_dummies(edges["color"]) pd.get_dummies(edges[["color"]])
- 1개면 그냥 출력
- 2개면 새로운 데이터프레임을 생성한것임
- 정수형 데이터 3,4,5를 M,L,XL로 변경
edges["weight"] = 3, 4, 5
weight_dict = {3:"M", 4:"L", 5:"XL"}
edges["weight_sign"] = edges["weight"].map(weight_dict)
weight_sign = pd.get_dummies(edges["weight_sign"])
바인딩
bins = [0, 25, 50, 75, 100]
group_names = ['Low', 'Okay', 'Good', 'Great']
categories = pd.cut(df['postTestScore'], bins, labels=group_names)
정규화 : feature normalization
- 데이터 간 범위 맞추는 것 (브로드캐스팅 개념)
- 평균을 0으로, 표준편차를 1로
- 최소값과 최대값 : 0.0~1.0의 범위로
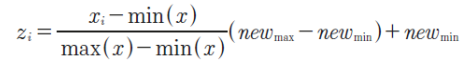
- z-score 정규화
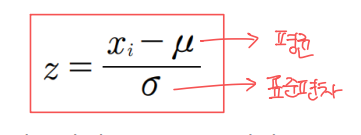
반응형
'dev-log > cs' 카테고리의 다른 글
| 정보보호 관리체계 (0) | 2024.04.26 |
|---|---|
| [양자 컴퓨팅과 보안] 수학적 배경 지식 (0) | 2024.04.17 |
| [양자 컴퓨팅과 보안] 양자 알고리즘 (0) | 2024.04.16 |
| [양자 컴퓨팅과 보안] 양자 게이트 (0) | 2024.04.16 |
| [양자 컴퓨팅과 보안] 큐빗 (0) | 2024.04.16 |



