[알고리즘] Tree (Prim, Kruskal)

그래프 용어

• 비방향성 그래프 : G=(V, E)
  • V : 정점 vertex의 집합
  • E : 연결 선 edge의 집합
• 연결 그래프
  • 두 정점 사이에도 경로가 존재하는 그래프
• 트리 (tree)
  • 비순환적
  • 비방향성
• 뿌리 있는 트리(rooted tree)
  • 한 정점이 뿌리로 지정되어있는 트리
• 순환적 그래프 (cyclic graph)
• 비순환적 그래프 (acyclic graph)

Spanning Tree (신장 트리)

: G(V, E)가 비방향성 연결 그래프일 때, G의 부분 그래프인 T(V, E’)를 G의 spanning tree라고 한다

⇒ T : tree, E’ : E의 부분집합 (E의 일부분)

⇒ 모든 정점을 포함하면서, cycle은 되지 않아 tree가 된 G의 부분 그래프

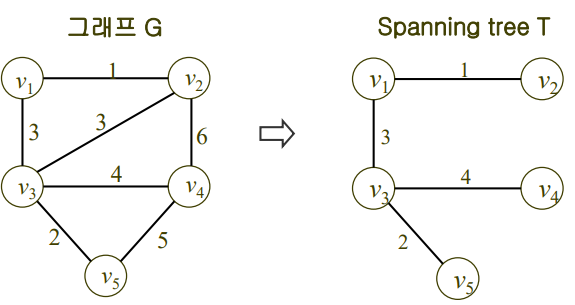
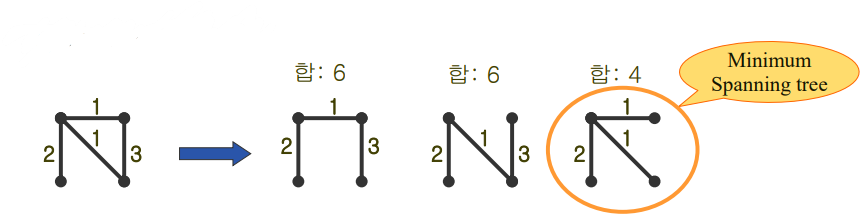
Minimum Spanning Tree (최소 비용 신장 트리)

• E’의 합이 최소가 되도록 tree를 만드는 것
• 도로 건설 / 통신 전화선 / 배관의 길이가 최소가 되도록 연결하는 문제

• 

해결 방법

• Greedy 알고리즘의 Prim’s / Kruskal’s 알고리즘 사용
• 표현 W[a][b] : 정점 a와 b 사이의 가중치
  • x : a와 b 사이 이음선이 있다면, 그 가중치를 x로 한다.
  • ∞ : a와 b 사이 이음선이 없으면 무한대로 한다.
  • 0 : a=b이면 거리는 0이다.
• 과정
  • selection : 적절한 선정 절차에 의해 하나의 edge선정
  • feasibility : 선정한 edge를 최종(F 집합)에 추가시켜도 cycle이 생기지 않는지 확인. cycle이 생기지 않으면 F에 추가
  • 해답 점검: T=(V, F)가 신장트리(minimum spanning tree)이면 T가 결론

Prim’s 알고리즘 vs Kruskal’s 알고리즘

• Prim : 임의의 정점으로 시작하여 가까운 정점 선택
  • V 집합 : 정점의 집합 / Y 집합 : 선정된 정점의 집합 / F 집합 : 선정된 정점을 잇는 연결선의 가중치의 집합
  • 연결된 점에서 가장 작은 가중치(연결선)를 가진 연결선의 정점을 집합 Y에 포함시킨다
  • 이 때 정점은 V-Y에 속해있다
  • cycle을 형성하는 정점은 포함하지 않는다
• Kruskal : 작은 가중치(연결 선) 순서로 정렬 후 적은 선 부터 연결
  • V 집합 : 정점의 집합 / Y 집합 : 선정된 정점의 집합 / F 집합 : 선정된 정점을 잇는 연결선의 가중치의 집합
  • ⇒ 모든 원소는 서로소이다.
  • 가중치(연결 선)를 순서대로 정렬한다
  • 정점은 모두 각각의 집합으로 본다
  • 작은 가중치(연결 선)부터 차례로 합집합 F로 포함시킨다
  • 정점은 합집합 V에 포함시킨다
  • cycle을 형성하는 연결 선은 포함하지 않는다

⇒ 어떤 방법을 써도 minimum spanning tree의 형태는 같지만, 과정의 차이가 있음

⇒ 사용되는 경우에 따라 시간복잡도가 달라지므로, 하나만 선택할 수 없다.

• prim : 거의 모든 정점(vertex)가 edge들로 연결된 경우 (edge가 많은 경우)
• kruskal : 정점의 수가 n일 때, edge 수가 n^2보다 n에 가까운 경우 (edge가 적은 경우)